Rumus cepat menghitung luas permukaan bangun ruang merupakan kunci untuk menyelesaikan berbagai permasalahan geometri, baik dalam konteks akademis maupun aplikasi praktis sehari-hari. Memahami rumus-rumus ini memungkinkan kita untuk menghitung luas permukaan kubus, balok, tabung, kerucut, prisma, limas, dan bola dengan efisien dan akurat. Artikel ini akan membahas secara detail rumus-rumus tersebut, dilengkapi dengan contoh perhitungan dan ilustrasi yang mudah dipahami.
Dari bangun ruang sederhana seperti kubus dan balok hingga bangun ruang yang lebih kompleks seperti kerucut dan limas, pemahaman yang mendalam tentang rumus luas permukaan akan membuka pintu untuk menyelesaikan berbagai masalah pengukuran dan desain. Dengan langkah-langkah perhitungan yang terstruktur dan ilustrasi yang jelas, artikel ini bertujuan untuk memberikan pemahaman komprehensif tentang bagaimana menghitung luas permukaan berbagai bangun ruang.
Rumus Luas Permukaan Kubus dan Balok
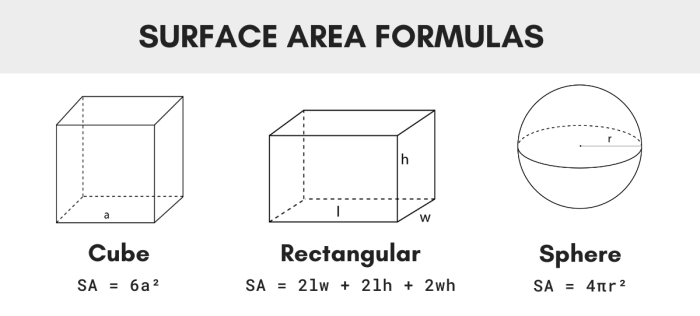
Menghitung luas permukaan bangun ruang merupakan keterampilan dasar dalam geometri. Memahami rumus dan penerapannya sangat penting dalam berbagai bidang, mulai dari arsitektur hingga teknik. Artikel ini akan membahas rumus luas permukaan kubus dan balok secara detail, dilengkapi dengan contoh perhitungan dan ilustrasi.
Rumus Luas Permukaan Kubus
Kubus merupakan bangun ruang tiga dimensi yang dibatasi oleh enam sisi berbentuk persegi yang kongruen (sama besar dan bentuk). Luas permukaan kubus adalah jumlah luas keenam sisi tersebut. Rumusnya dapat ditulis sebagai:
Luas Permukaan Kubus = 6s2
dimana s adalah panjang rusuk kubus.
Contoh Perhitungan Luas Permukaan Kubus
Misalnya, kita memiliki kubus dengan panjang rusuk 5 cm. Langkah-langkah perhitungan luas permukaannya adalah:
- Tentukan panjang rusuk (s) = 5 cm
- Substitusikan nilai s ke dalam rumus: Luas Permukaan = 6 x (5 cm)2
- Hitung: Luas Permukaan = 6 x 25 cm 2 = 150 cm 2
Jadi, luas permukaan kubus dengan panjang rusuk 5 cm adalah 150 cm 2.
Rumus Luas Permukaan Balok
Balok merupakan bangun ruang tiga dimensi yang dibatasi oleh enam sisi berbentuk persegi panjang. Luas permukaan balok adalah jumlah luas keenam sisi tersebut. Rumusnya dapat ditulis sebagai:
Luas Permukaan Balok = 2(pl + pt + lt)
dimana p adalah panjang, l adalah lebar, dan t adalah tinggi balok.
Contoh Perhitungan Luas Permukaan Balok
Misalnya, kita memiliki balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm. Langkah-langkah perhitungan luas permukaannya adalah:
- Tentukan panjang (p) = 10 cm, lebar (l) = 5 cm, dan tinggi (t) = 3 cm
- Substitusikan nilai p, l, dan t ke dalam rumus: Luas Permukaan = 2((10 cm)(5 cm) + (10 cm)(3 cm) + (5 cm)(3 cm))
- Hitung: Luas Permukaan = 2(50 cm2 + 30 cm 2 + 15 cm 2) = 2(95 cm 2) = 190 cm 2
Jadi, luas permukaan balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm adalah 190 cm 2.
Tabel Perbandingan Rumus Luas Permukaan Kubus dan Balok
| Bangun Ruang | Rumus Luas Permukaan | Variabel | Penjelasan Variabel |
|---|---|---|---|
| Kubus | 6s2 | s | Panjang rusuk |
| Balok | 2(pl + pt + lt) | p, l, t | Panjang, lebar, tinggi |
Ilustrasi Kubus dan Balok
Kubus: Bayangkan sebuah dadu. Keenam sisinya berbentuk persegi dan identik. Untuk menghitung luas permukaannya, kita hitung luas satu sisi (s 2) lalu dikalikan enam karena ada enam sisi yang sama.
Balok: Bayangkan sebuah kotak sepatu. Terdapat tiga pasang sisi yang berhadapan dan kongruen. Satu pasang sisi memiliki luas (p x l), satu pasang sisi memiliki luas (p x t), dan satu pasang sisi memiliki luas (l x t). Jumlah luas keenam sisi inilah yang merupakan luas permukaan balok.
Rumus Luas Permukaan Tabung dan Kerucut
Menghitung luas permukaan bangun ruang, khususnya tabung dan kerucut, merupakan keterampilan penting dalam geometri. Memahami rumus dan penerapannya akan memudahkan kita dalam menyelesaikan berbagai permasalahan terkait volume dan dimensi bangun ruang ini. Berikut penjelasan detail rumus dan contoh perhitungannya.
Rumus Luas Permukaan Tabung dan Kerucut
Rumus luas permukaan tabung dan kerucut melibatkan beberapa variabel yang perlu dipahami. Pemahaman yang baik terhadap variabel-variabel ini akan mempermudah proses perhitungan.
- Tabung: Luas permukaan tabung terdiri dari luas permukaan selimut dan dua lingkaran alas. Rumusnya adalah: L total = 2πr(r + t), di mana:
- L total = Luas permukaan total tabung
- π = Konstanta phi (≈ 3,14)
- r = Jari-jari alas tabung
- t = Tinggi tabung
- Kerucut: Luas permukaan kerucut terdiri dari luas permukaan selimut dan luas lingkaran alas. Rumusnya adalah: L total = πr(r + s), di mana:
- L total = Luas permukaan total kerucut
- π = Konstanta phi (≈ 3,14)
- r = Jari-jari alas kerucut
- s = Garis pelukis kerucut (panjang garis dari puncak kerucut ke titik pada keliling alas)
Perbedaan Luas Permukaan Selimut dan Luas Permukaan Total Tabung
Pada tabung, luas permukaan selimut merupakan luas permukaan bagian samping tabung tanpa alas dan tutup. Rumusnya adalah 2πrt. Luas permukaan total tabung meliputi luas permukaan selimut ditambah luas kedua lingkaran alas (2πr²). Jadi, luas permukaan total lebih besar daripada luas permukaan selimut.
Contoh Perhitungan Luas Permukaan Tabung
Hitung luas permukaan total tabung dengan jari-jari 7 cm dan tinggi 10 cm.
- Tentukan nilai variabel yang diketahui: r = 7 cm, t = 10 cm, π ≈ 3,14
- Substitusikan nilai ke dalam rumus: Ltotal = 2πr(r + t) = 2
- 3,14
- 7 (7 + 10)
- Hitung hasilnya: L total = 2
- 3,14
- 7
- 17 = 747,32 cm²
Jadi, luas permukaan total tabung tersebut adalah 747,32 cm².
Contoh Perhitungan Luas Permukaan Kerucut
Hitung luas permukaan total kerucut dengan jari-jari 4 cm dan tinggi 6 cm. Pertama, kita perlu menghitung garis pelukis (s) menggunakan teorema Pythagoras: s² = r² + t².
- Hitung garis pelukis (s): s = √(r² + t²) = √(4² + 6²) = √(16 + 36) = √52 ≈ 7,21 cm
- Tentukan nilai variabel yang diketahui: r = 4 cm, s ≈ 7,21 cm, π ≈ 3,14
- Substitusikan nilai ke dalam rumus: Ltotal = πr(r + s) = 3,14 – 4 (4 + 7,21)
- Hitung hasilnya: L total = 3,14
- 4
- 11,21 ≈ 140,6 cm²
Jadi, luas permukaan total kerucut tersebut adalah sekitar 140,6 cm².
Tips mengingat rumus: Bayangkan tabung sebagai dua lingkaran (2πr²) dan satu persegi panjang yang dibentuk dari selimut (2πrt). Untuk kerucut, bayangkan lingkaran alas (πr²) dan sebuah juring lingkaran yang membentuk selimut (πrs).
Rumus Luas Permukaan Prisma dan Limas
Menghitung luas permukaan bangun ruang, khususnya prisma dan limas, membutuhkan pemahaman yang baik terhadap rumus dan komponen bangun ruang tersebut. Artikel ini akan membahas rumus luas permukaan prisma dan limas, disertai contoh perhitungan untuk memperjelas pemahaman.
Rumus Luas Permukaan Prisma Segitiga dan Limas Segitiga
Rumus luas permukaan bangun ruang ini didasarkan pada penjumlahan luas semua sisi penyusun bangun ruang tersebut. Untuk prisma segitiga, luas permukaannya adalah jumlah luas dua buah alas segitiga dan tiga buah sisi tegak berbentuk persegi panjang. Sedangkan untuk limas segitiga, luas permukaannya adalah jumlah luas satu buah alas segitiga dan tiga buah sisi tegak berbentuk segitiga.
Berikut rincian variabel yang digunakan:
- Prisma Segitiga:
- Lp = 2La + 3Ls, di mana:
- Lp = Luas Permukaan Prisma
- La = Luas Alas Segitiga
- Ls = Luas Sisi Tegak (persegi panjang)
- Limas Segitiga:
- Lp = La + 3Ls, di mana:
- Lp = Luas Permukaan Limas
- La = Luas Alas Segitiga
- Ls = Luas Sisi Tegak (segitiga)
Contoh Perhitungan Luas Permukaan Prisma Segitiga, Rumus cepat menghitung luas permukaan bangun ruang
Misalkan kita memiliki prisma segitiga dengan alas segitiga siku-siku berukuran 3 cm, 4 cm, dan 5 cm, serta tinggi prisma 10 cm. Langkah-langkah perhitungannya adalah:
- Hitung luas alas segitiga (La): La = 1/2 x alas x tinggi = 1/2 x 3 cm x 4 cm = 6 cm²
- Hitung luas sisi tegak (Ls): Karena alasnya segitiga siku-siku, maka terdapat 3 sisi tegak. Dua sisi tegak memiliki ukuran 10 cm x 3 cm = 30 cm² dan satu sisi tegak berukuran 10 cm x 4 cm = 40 cm². Maka Ls = (30 + 30 + 40) cm² = 100 cm²
- Hitung luas permukaan prisma (Lp): Lp = 2La + 3Ls = 2(6 cm²) + 100 cm² = 112 cm²
Jadi, luas permukaan prisma segitiga tersebut adalah 112 cm².
Contoh Perhitungan Luas Permukaan Limas Segitiga
Misalkan kita memiliki limas segitiga dengan panjang sisi alas 6 cm dan tinggi limas 8 cm. Kita asumsikan alasnya berupa segitiga sama sisi. Langkah-langkah perhitungannya adalah:
- Hitung luas alas segitiga (La): Kita perlu mencari tinggi segitiga alas terlebih dahulu. Karena segitiga sama sisi, tinggi segitiga = √3/2 x sisi = √3/2 x 6 cm ≈ 5.2 cm. Maka La = 1/2 x alas x tinggi = 1/2 x 6 cm x 5.2 cm ≈ 15.6 cm²
- Hitung luas sisi tegak (Ls): Tinggi segitiga sisi tegak = √(tinggi limas² + (1/2 sisi alas)²) = √(8² + 3²) ≈ 8.54 cm. Maka Ls = 1/2 x alas x tinggi = 1/2 x 6 cm x 8.54 cm ≈ 25.62 cm². Karena ada 3 sisi tegak, total luas sisi tegak = 3 x 25.62 cm² ≈ 76.86 cm²
- Hitung luas permukaan limas (Lp): Lp = La + 3Ls ≈ 15.6 cm² + 76.86 cm² ≈ 92.46 cm²
Jadi, luas permukaan limas segitiga tersebut adalah sekitar 92.46 cm².
Perbandingan Rumus Luas Permukaan Prisma dan Limas
| Bangun Ruang | Rumus Luas Permukaan | Penjelasan | Catatan |
|---|---|---|---|
| Prisma Segitiga | 2La + 3Ls | 2 kali luas alas segitiga ditambah 3 kali luas sisi tegak (persegi panjang) | Bentuk dan ukuran sisi tegak dapat bervariasi tergantung bentuk alas. |
| Limas Segitiga | La + 3Ls | Luas alas segitiga ditambah 3 kali luas sisi tegak (segitiga) | Bentuk dan ukuran sisi tegak dapat bervariasi tergantung bentuk alas. |
Langkah-Langkah Umum Menghitung Luas Permukaan Prisma dan Limas
Secara umum, menghitung luas permukaan prisma dan limas melibatkan langkah-langkah berikut:
- Identifikasi bentuk bangun ruang dan komponen-komponennya (alas dan sisi tegak).
- Hitung luas masing-masing komponen (alas dan sisi tegak) dengan rumus geometri yang sesuai.
- Jumlahkan luas semua komponen untuk mendapatkan luas permukaan total.
Rumus Luas Permukaan Bola
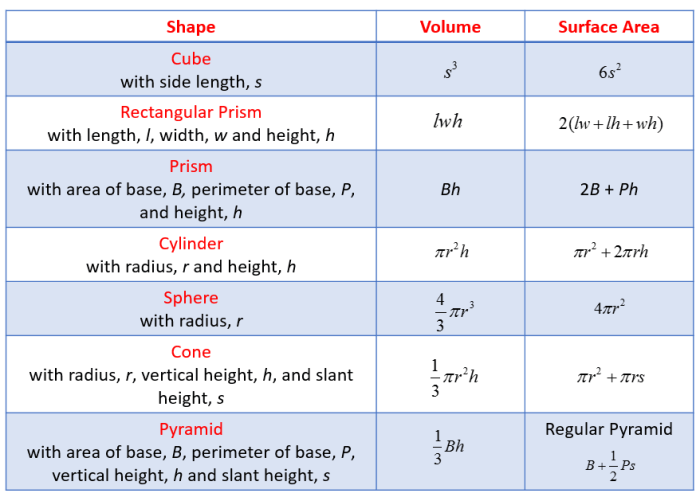
Menghitung luas permukaan bola mungkin terdengar rumit, namun sebenarnya cukup sederhana jika kita memahami rumusnya. Luas permukaan bola berkaitan erat dengan jari-jari bola tersebut, dan dengan memahami rumus ini, kita dapat menghitung luas permukaan berbagai objek berbentuk bola, mulai dari bola sepak hingga planet-planet di tata surya kita.
Rumus Luas Permukaan Bola dan Variabelnya
Rumus luas permukaan bola dinyatakan sebagai:
L = 4πr²
di mana:
- L mewakili luas permukaan bola.
- r mewakili jari-jari bola.
- π (pi) adalah konstanta matematika dengan nilai aproksimasi 3,14159.
Rumus ini menunjukkan bahwa luas permukaan bola berbanding lurus dengan kuadrat jari-jarinya. Artinya, jika jari-jari bola dilipatgandakan, luas permukaannya akan menjadi empat kali lipat.
Contoh Perhitungan Luas Permukaan Bola
Mari kita hitung luas permukaan bola dengan jari-jari 5 cm. Berikut langkah-langkahnya:
- Tuliskan rumus: L = 4πr²
- Substitusikan nilai r = 5 cm: L = 4π(5 cm)²
- Hitung kuadrat jari-jari: L = 4π(25 cm²)
- Kalikan dengan 4π: L = 100π cm²
- Gunakan nilai π ≈ 3,14: L ≈ 100 x 3,14 cm²
- Hasil akhir: L ≈ 314 cm²
Jadi, luas permukaan bola dengan jari-jari 5 cm adalah sekitar 314 cm².
Ilustrasi dan Penerapan Rumus pada Bola
Bayangkan bola dipotong-potong menjadi banyak irisan kecil yang sangat tipis. Jika irisan-irisan tersebut diratakan, kita akan mendapatkan bentuk yang mendekati persegi panjang. Panjang persegi panjang ini akan mendekati keliling lingkaran besar bola (2πr), sedangkan lebarnya mendekati jari-jari bola (r). Luas satu irisan akan mendekati (2πr) x r = 2πr². Karena ada banyak irisan yang mendekati jumlah 2, maka luas totalnya mendekati 4πr².
Mengubah Rumus jika Diketahui Diameter
Jika yang diketahui adalah diameter (d) bola, bukan jari-jari, kita dapat menggunakan hubungan d = 2r. Dengan demikian, rumus luas permukaan bola dapat ditulis ulang sebagai:
L = πd²
Dengan menggunakan rumus ini, perhitungan akan menjadi lebih singkat jika diameter sudah diketahui.
Tips dan Trik Mengingat Rumus Luas Permukaan Bola
Cara paling efektif untuk mengingat rumus ini adalah dengan sering berlatih mengerjakan soal. Visualisasikan bola dan bayangkan bagaimana rumus tersebut merepresentasikan luas permukaannya. Mengasosiasikan angka 4 dan kuadrat jari-jari (r²) dengan bentuk bola juga dapat membantu mengingat rumus ini dengan lebih mudah.
Penerapan Rumus Luas Permukaan Bangun Ruang dalam Kehidupan Sehari-hari
Memahami rumus luas permukaan bangun ruang bukan hanya sekadar pengetahuan matematika semata. Kemampuan ini memiliki aplikasi praktis yang luas dalam berbagai aspek kehidupan sehari-hari, membantu kita dalam memecahkan masalah dan membuat keputusan yang lebih efisien. Berikut beberapa contoh penerapannya.
Contoh Penerapan Rumus Luas Permukaan Bangun Ruang
Rumus luas permukaan bangun ruang digunakan untuk menghitung luas total permukaan suatu bangun ruang. Penggunaan rumus ini sangat penting dalam berbagai konteks, dari perencanaan pembangunan hingga pengemasan barang.
- Mengecat Tembok Rumah: Sebuah rumah memiliki dinding berbentuk persegi panjang dengan tinggi 3 meter, panjang 5 meter, dan lebar 4 meter. Untuk mengecat seluruh dinding, kita perlu menghitung luas permukaan total dinding tersebut. Dengan menggunakan rumus luas permukaan balok (2 x (panjang x lebar) + 2 x (panjang x tinggi) + 2 x (lebar x tinggi)), kita dapat menentukan jumlah cat yang dibutuhkan.
Dalam hal ini, luas permukaan dinding adalah 2 x (5m x 4m) + 2 x (5m x 3m) + 2 x (4m x 3m) = 94 meter persegi.
- Membuat Kemasan Produk: Sebuah perusahaan ingin membuat kemasan berbentuk kubus untuk produknya. Agar kemasan tersebut dapat memuat produk dengan ukuran tertentu dan efisien dalam penggunaan bahan, perusahaan perlu menghitung luas permukaan kubus (6 x sisi x sisi). Misalnya, jika sisi kubus adalah 10 cm, luas permukaannya adalah 6 x 10cm x 10cm = 600 cm persegi. Informasi ini penting untuk menentukan jumlah bahan yang dibutuhkan dan biaya produksi.
- Membangun Kolam Renang: Dalam membangun kolam renang berbentuk balok, perhitungan luas permukaan dinding dan dasar kolam sangat penting untuk menentukan jumlah keramik atau bahan pelapis yang dibutuhkan. Misalnya, sebuah kolam renang dengan panjang 10 meter, lebar 5 meter, dan kedalaman 2 meter membutuhkan perhitungan luas permukaan balok untuk menentukan jumlah keramik yang dibutuhkan untuk melapisi dinding dan dasar kolam. Luas permukaan yang perlu dilapisi adalah 2 x (10m x 5m) + 2 x (10m x 2m) + 2 x (5m x 2m) + (10m x 5m) = 200 meter persegi (menambahkan luas dasar kolam).
Kesimpulan Pentingnya Memahami Rumus Luas Permukaan Bangun Ruang
Memahami dan mampu menerapkan rumus luas permukaan bangun ruang sangat penting dalam berbagai aspek kehidupan, mulai dari pekerjaan konstruksi hingga industri kemasan. Kemampuan ini memungkinkan kita untuk melakukan perencanaan yang lebih efisien, mengoptimalkan penggunaan sumber daya, dan menghasilkan solusi yang efektif.
Tabel Ringkasan Contoh Penerapan
| Bangun Ruang | Permasalahan | Solusi |
|---|---|---|
| Balok (Dinding Rumah) | Menghitung jumlah cat yang dibutuhkan untuk mengecat dinding rumah. | Hitung luas permukaan balok menggunakan rumus 2 x (panjang x lebar) + 2 x (panjang x tinggi) + 2 x (lebar x tinggi). |
| Kubus (Kemasan Produk) | Menentukan jumlah bahan yang dibutuhkan untuk membuat kemasan produk berbentuk kubus. | Hitung luas permukaan kubus menggunakan rumus 6 x sisi x sisi. |
| Balok (Kolam Renang) | Menghitung jumlah keramik yang dibutuhkan untuk melapisi kolam renang berbentuk balok. | Hitung luas permukaan balok, termasuk dasar kolam, menggunakan rumus yang dimodifikasi sesuai kebutuhan. |
Profesi yang Menggunakan Perhitungan Luas Permukaan Bangun Ruang
Banyak profesi yang memanfaatkan perhitungan luas permukaan bangun ruang dalam pekerjaan mereka. Dua contohnya adalah:
- Arsitek: Arsitek menggunakan perhitungan luas permukaan untuk menentukan jumlah material yang dibutuhkan dalam membangun sebuah bangunan, seperti jumlah batu bata, cat, atau ubin. Mereka juga menggunakannya untuk menghitung biaya material dan perencanaan anggaran.
- Insinyur Sipil: Insinyur sipil menggunakan perhitungan luas permukaan untuk merancang berbagai struktur, seperti jembatan, bendungan, dan jalan raya. Perhitungan ini penting untuk memastikan struktur tersebut kuat, stabil, dan tahan lama.
Menguasai rumus cepat menghitung luas permukaan bangun ruang bukan hanya sekadar memahami rumus matematika, tetapi juga tentang kemampuan untuk menerapkannya dalam berbagai situasi. Kemampuan ini sangat berharga, baik untuk memecahkan soal-soal matematika, maupun untuk menyelesaikan permasalahan praktis dalam berbagai bidang pekerjaan dan kehidupan sehari-hari. Dengan pemahaman yang kuat tentang konsep-konsep dasar dan latihan yang cukup, siapa pun dapat menguasai rumus-rumus ini dan memanfaatkannya secara efektif.
FAQ Terkini: Rumus Cepat Menghitung Luas Permukaan Bangun Ruang
Apa yang dimaksud dengan luas permukaan selimut?
Luas permukaan selimut adalah luas permukaan bagian samping suatu bangun ruang, tanpa memperhitungkan alas dan atapnya.
Bagaimana cara menghitung luas permukaan bangun ruang yang tidak beraturan?
Untuk bangun ruang tidak beraturan, biasanya diperlukan pendekatan dengan metode integral kalkulus atau pendekatan numerik lainnya.
Apakah ada software atau aplikasi yang dapat membantu menghitung luas permukaan bangun ruang?
Ya, terdapat beberapa software dan aplikasi matematika, CAD, atau aplikasi kalkulator yang dapat membantu menghitung luas permukaan bangun ruang.

